Seed de 12 ou 24 palavras? Veja esta análise
Neste artigo pretendemos comparar a segurança das seed phrases de 12 e 24 palavras e entender o processo de criação da chave privada, assim como abordar os possíveis ataques, e trazer recomendações de segurança.

A segurança das criptomoedas é um tema crucial no mundo digital atual. Desde a criação do Bitcoin em 2009, o universo das criptomoedas tem crescido exponencialmente, oferecendo liberdade financeira sem precedentes para milhões de pessoas ao redor do mundo. No entanto, essa liberdade vem acompanhada de uma grande responsabilidade: a proteção dos ativos digitais.
Neste artigo pretendemos comparar a segurança das seed phrases de 12 e 24 palavras e entender o processo de criação da chave privada, assim como abordar os possíveis ataques, e trazer recomendações de segurança.
Assuntos abordados:
- Padrão BIP39
- Entropia
- Seed Phrases
- Colisões e Ataque às Seed Phrases
- Chaves privadas e Curvas Elípticas
- Colisões e ataques às Chaves Privadas
- Era Pré-Quântica e Pós-Quântica
- A Importância de uma Passphrase Forte
- Recomendações de segurança
Seed Phrases: O Básico
Um dos métodos mais eficazes e comuns para garantir a segurança das criptomoedas é através do uso de seed phrases, ou frases-semente. Essas frases são sequências de palavras aleatórias, escolhidas de uma lista predefinida conhecida como BIP39, utilizadas para gerar chaves privadas. Este padrão foi desenvolvido para padronizar a criação e recuperação de carteiras de criptomoedas, proporcionando uma forma segura e consistente de geração de chaves privadas.
As chaves privadas são fundamentais, pois permitem o acesso e o controle direto sobre os ativos criptográficos. A importância de uma seed phrase segura não pode ser subestimada, pois existem inúmeros casos de indivíduos que perderam suas criptomoedas devido ao extravio ou comprometimento de suas seed phrases.
Padrão BIP39
O padrão BIP39 é crucial porque define uma metodologia segura e universal para a criação de seed phrases. Isso garante que, independentemente da carteira ou software utilizado, os usuários possam sempre recuperar seus ativos desde que possuam a seed phrase correta. O BIP39 também facilita a interoperabilidade entre diferentes carteiras e plataformas de criptomoedas.
Exemplo de seed com 12 palavras
off energy lounge crisp library inmate accident occur boring aunt cherry gallery
Esta frase é convertida em um valor binário e calculado o hash \(sha256(mnemônico)\), resultando em uma master key que pode gerar diversas chaves privadas e públicas (processo descrito mais abaixo). Se a seed phrase fosse de 24 palavras, o processo seria o mesmo, mas com um nível de segurança exponencialmente maior devido ao aumento da entropia.
Entropia e Segurança
A entropia mede a imprevisibilidade de um sistema. No contexto de seed phrases, quanto maior a entropia, mais difícil é adivinhar a sequência correta de palavras. Uma seed phrase de 12 palavras possui aproximadamente 128 bits de entropia, enquanto a de 24 palavras tem 256 bits. Para compreender a diferença entre esses níveis de entropia, é crucial entender que a diferença não é linear, mas exponencial.
Uma seed phrase de 12 palavras possui cerca de \(2^{128}\) combinações possíveis. Embora isso pareça um número imenso, é importante entender que \(2^{128}\) não é a metade de \(2^{256}\). Na realidade, \(2^{128}\) é a metade de \(2^{129}\). O número de combinações possíveis para uma seed phrase de 24 palavras é de aproximadamente \(2^{256}\), que é astronomicamente maior que \(2^{128}\). Esse aumento exponencial na quantidade de combinações torna a seed phrase de 24 palavras extremamente mais segura contra ataques de força bruta.
Para simplificar, vamos calcular \((2^2)=4\) e \((2^3)=8\). Veja que o primeiro cálculo resulta em metade do segundo, enquanto ao expoente foi adicionado apenas 1.
Exemplo Comparativo
Para ilustrar melhor, veja a comparação abaixo:
| Seed Phrase | Bits de Entropia | Combinações Possíveis |
|---|---|---|
| 12 palavras | 128 bits | \(2^{128}\) \(\approx 3.4 \times 10^{38}\) |
| 24 palavras | 256 bits | \(2^{256}\) \(\approx 1.1 \times 10^{77}\) |
Exemplos de Aplicações em Segurança da Informação
- Senhas: Senhas com maior entropia são mais difíceis de adivinhar. Por exemplo, uma senha de 8 caracteres normalmente tem menos entropia que uma senha de 16 caracteres (existem excessões e vamos explorar mais adiante), especialmente se a segunda incluir uma combinação de letras maiúsculas, minúsculas, números e símbolos.
- Chaves Criptográficas: Chaves criptográficas usadas em protocolos de segurança (como SSL/TLS) possuem alta entropia para garantir que não possam ser facilmente quebradas.
Força Bruta: Adivinhando a Agulha no Palheiro
Imagine um invasor tentando adivinhar sua seed phrase. É como procurar uma agulha em um palheiro. Vamos utilizar algumas analogias e comparações práticas para entender melhor a diferença entre adivinhar uma seed phrase de 12 palavras e uma de 24 palavras.
Imagine que você tem duas salas cheias de combinações de palavras (palheiros):
- 12 palavras: Este palheiro é enorme, contendo aproximadamente 4.4 quintilhões de combinações ou \(4.4 \times (10^{18}) = 2601150623552800702891545856\). Embora pareça muito, um invasor com poder computacional suficiente poderia, teoricamente, encontrar a combinação correta em um tempo relativamente razoável, dado o avanço contínuo da capacidade de processamento.
- 24 palavras: Agora imagine um palheiro colossal, com 620 sextilhões de combinações ou \(6.2 \times (10^{23}) = 41731122174410236047796743722730466018640279171473593600\). Este palheiro é tão vasto que ultrapassa nossa capacidade de compreensão e, mesmo com o melhor computador do mundo, adivinhar a sequência correta levaria mais tempo que a existência do universo.
Seed Phrase de 12 Palavras
Isso é um número incrivelmente grande, mas com poder computacional suficiente, teoricamente é possível forçar a entrada. Vamos colocar isso em perspectiva:
- Tempo Necessário com Supercomputador Moderno: Supondo que um supercomputador moderno possa testar \(10^{17}\) combinações por segundo, levaria cerca de:
\[ \frac {2^{128}} {10^{17}} \approx 3.4 \times 10^{21} \text segundos \approx 10^{14} \text anos \]
Para contextualizar, \(10^{14}\) anos é cerca de 10.000 vezes a idade atual do universo (aproximadamente 13.8 bilhões de anos).
Seed Phrase de 24 Palavras
Já uma seed phrase de 24 palavras tem cerca de \(2^{256}\) combinações possíveis, o que equivale a aproximadamente 620 sextilhões \(6.2 \times (10^{23})\) de combinações. Este número é tão grande que ultrapassa nossa capacidade de compreensão. Mesmo com o melhor computador do mundo, adivinhar a sequência correta levaria um tempo absurdamente maior. Vamos ver o cálculo:
- Tempo Necessário com Supercomputador Moderno: Com o mesmo supercomputador que pode testar \(10^{17}\) combinações por segundo, o tempo necessário seria:
\[ \frac {2^{128}} {10^{17}} \approx 1.1 \times 10^{60} \text segundos \approx 10^{52} \text anos \]
Para contextualizar, \(10^{52}\) anos é uma quantidade de tempo inimaginável, muito além da idade do universo.
Comparações Práticas
Para tornar isso mais didático, considere as seguintes comparações:
- Idade do Universo: Cerca de \(10^{10}\) anos.
- Grãos de Areia na Terra: Estima-se que haja cerca de \(10^{20}\) grãos de areia na Terra. A quantidade de combinações para uma seed phrase de 24 palavras é muito maior do que o número de grãos de areia em nosso planeta.
- Átomos no Universo Observável: O número de átomos no universo observável é estimado em torno de \(10^{80}\).
Curiosidade: Processo de Derivação das Chaves Privadas
As seed phrases funcionam através de um processo de derivação criptográfica que transforma a sequência de palavras em uma chave privada. Este processo pode ser dividido em várias etapas:
- Seleção das Palavras: As palavras são selecionadas da lista BIP39 (que possui 2048 palavras) para formar a seed phrase.
- Cálculo do Hash: A seed phrase é transformada em um valor binário, que é posteriormente processado pelo algoritmo
SHA-256 paragerar um hash. - Derivação da Master Key: O hash é usado como entrada para um algoritmo de derivação de chave, como o
HMAC-SHA512, para gerar uma master key. - Gerenciamento de Sub-chaves: A master key pode ser usada para gerar uma hierarquia de sub-chaves (usando o padrão BIP32), que são as chaves privadas e públicas usadas em transações de criptomoedas.
Colisão e ataque à Seed Phrase
Conceito do Ataque de Aniversário (Birthday Attack)
Este conceito é baseado no paradoxo do aniversário, que ilustra como a probabilidade de colisões aumenta rapidamente com o número de elementos.
No contexto de criptografia, uma colisão ocorre quando duas informações (entradas) diferentes produzem a mesma saída de hash. Este tipo de ataque é especialmente relevante em sistemas onde a função hash é uma parte crucial da segurança, como na geração de seed phrases.
Exemplos de Exploração de Colisões
Suponha que um invasor queira explorar colisões em seed phrases de 12 palavras. Ele precisaria gerar e comparar um grande número de seed phrases até encontrar uma colisão. O número de tentativas necessárias para encontrar uma colisão é proporcional ao valor da raiz quadrada do número total de combinações possíveis \(\sqrt{N}\) .
- Seed Phrase de 12 Palavras:
- \(N=2^{128}\)
- Tentativas necessárias para colisão: \(\sqrt{2^{128}} = 2^{128/2} = 2^{64}\)
- Seed Phrase de 24 Palavras:
- \(N = 2^{256}\)
- Tentativas necessárias para colisão: \(\sqrt{2^{256}} = 2^{256/2} = 2^{128}\)
Com seed phrases de 12 palavras, que têm 128 bits de entropia, a chance de colisão (duas pessoas gerando a mesma sequência) é matematicamente possível, embora improvável, para um grande número de usuários. Em termos práticos, a probabilidade de duas seed phrases de 12 palavras colidirem após \(2^{64}\) tentativas é considerável (18446744073709551616 de tentativas), devido ao ataque de aniversário que se torna viável com alto poder de processamento.
Esta vulnerabilidade se torna mais significativa em cenários de múltiplos usuários, onde um grande número de seed phrases é gerado. É importante lembrar que nem sempre um endereço é criado por um usuário humano, mas por sistemas automatizados como exchanges, robôs de arbitragem, sistemas de coinjoin, wallets, etc.
Por outro lado, seed phrases de 24 palavras têm 256 bits de entropia. A entropia muito maior torna a probabilidade de colisões praticamente inexistente, mesmo considerando o ataque de aniversário. Com \(2^{256}\) combinações possíveis, a quantidade de tentativas necessárias para encontrar uma colisão é astronomicamente alta \(2^{128}\), tornando o sistema extremamente seguro contra esse tipo de ataque.
Cálculo Passo a Passo para um Ataque de Aniversário
Para colocar isso em perspectiva, o atual hashrate do Bitcoin é de 545 EH/s, mostrando que esse nível de computação é atualmente existente.
Número Total de Hashes Necessários (para \(2^{64}\)):
\[2^{64} \approx 1.8446744 \times 10^{19}\]
Taxa de Hashing:
\[545 \times 10^{18} \text{ hashes por segundo} = 5.45 \times 10^{20} \text{ hashes por segundo}\]
Tempo para Quebrar a Chave (em segundos):
\[\text{Tempo (em segundos)} = \frac{2^{64} \text{ hashes}}{5.45 \times 10^{20} \text{ hashes/segundo}}\]\[\text{Tempo (em segundos)} = \frac{1.8446744 \times 10^{19}}{5.45 \times 10^{20}}\]\[\text{Tempo (em segundos)} \approx 0.0338 \text{ segundos}\]
Converter Segundos para Anos:
\[\text{Tempo (em anos)} = \frac{0.0338 \text{ segundos}}{60 \times 60 \times 24 \times 365.25}\]\[\text{Tempo (em anos)} \approx 1.073 \times 10^{-9} \text{ anos}\]
Usando um ataque de aniversário com uma taxa de hashing de 545 EH/s para quebrar uma chave de \(2^{128}\) levaria aproximadamente 0.0338 segundos, o que é equivalente a aproximadamente \(1.073 \times 10^{-9}\) anos. Este é um período de tempo extremamente curto, indicando a eficácia do ataque de aniversário em reduzir a complexidade temporal.
Como comparação, usando um ataque de aniversário com uma taxa de hashing de 545 EH/s para quebrar uma chave de \(2^{256}\) levaria aproximadamente \(6.24 \times 10^{17}\) segundos, o que é equivalente a aproximadamente \(1.98 \times 10^{10}\) anos, ou cerca de 19,8 bilhões de anos.
No entanto, é crucial notar vários pontos importantes:
- Este ataque encontra colisões, não necessariamente a chave específica. É útil para criar colisões de hash, mas não para quebrar todos os tipos de sistemas criptográficos.
- O ataque de aniversário é um método probabilístico. O tempo calculado dá uma chance de >50% de encontrar uma colisão. Para ter quase certeza (por exemplo, 99,9% de probabilidade), precisaríamos executar o ataque por mais tempo.
- Isso assume que a função de hash se comporta de maneira ideal. Sistemas criptográficos no mundo real geralmente têm complexidades adicionais que podem tornar esse ataque mais difícil ou menos útil.
- A viabilidade de armazenar e comparar \(2^{64}\) hashes é uma consideração prática significativa que este cálculo teórico não aborda.
Argumento a Favor das 12 Palavras
Alguns especialistas argumentam que uma seed phrase de 12 palavras, que proporciona 128 bits de entropia, já oferece uma segurança suficiente contra ataques de força bruta com as capacidades computacionais atuais. Eles sustentam que a segurança do Bitcoin se baseia mais na dificuldade de resolver o Problema do Logaritmo Discreto de Curva Elíptica (ECDLP) do que na extensão da seed phrase. Assim, uma frase de 24 palavras não traria benefícios práticos adicionais em termos de segurança, mas aumentaria a complexidade para o usuário, piorando a usabilidade e aumentando a possibilidade de erros ao anotar as palavras.
Contra-Argumento
Embora uma seed phrase de 12 palavras ofereça segurança significativa, uma frase de 24 palavras aumenta a entropia para 256 bits, multiplicando exponencialmente as combinações possíveis e, portanto, a resistência a ataques de força bruta. Isso proporciona uma proteção extra contra avanços futuros no poder computacional e possíveis ameaças de computação quântica. Além disso, não consideram o Birthday Attack, que reduz exponencialmente o número de combinações necessárias para criar uma colisão.
Ainda, uma maior entropia minimiza os riscos associados a vulnerabilidades em geradores de números aleatórios ou avanços criptográficos imprevistos, garantindo a segurança dos ativos a longo prazo. A pequena inconveniência de lidar com uma frase mais longa é superada pelos benefícios de segurança, especialmente em um cenário tecnológico em constante evolução.
Sobre o risco de anotar as palavras com erro ou trocá-las de posição, eu costumo sugerir o procedimento de resetar/apagar a wallet recém criada e recuperá-la com o backup. Dessa forma fica fácil descobrir se há alguma falha ainda quando a wallet está vazia. Além disso, permite praticar a recuperação, diminuindo o stress na eventualidade de precisar restaurá-la no futuro.
Curvas Elípticas e Criptografia de Bitcoin
A criptografia de curvas elípticas é um tipo de criptografia que utiliza as propriedades matemáticas das curvas elípticas para criar chaves criptográficas seguras. A curva elíptica usada pelo Bitcoin é conhecida como secp256k1. Esta curva é definida pela seguinte equação:
\[ y^2 = x^3 + 7 \]
Quando representada utilizando números reais, ela aparenta a curva da imagem abaixo:
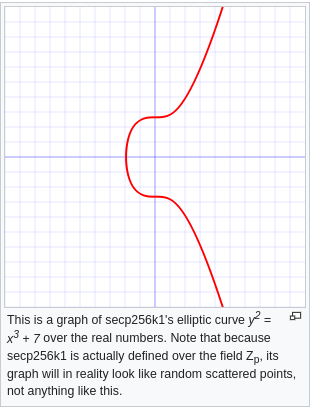
Mas na prática, ela acaba possuindo o seguinte formato, muito mais dispersa.
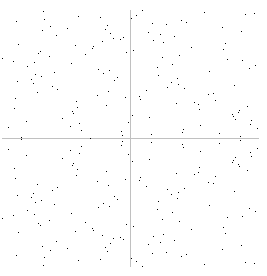
Embora geometricamente ela não faça mais sentido, ela ainda possui todas as propriedades necessárias (Pieter Wuille).
Propriedades das Curvas Elípticas
As curvas elípticas têm várias propriedades que as tornam adequadas para criptografia:
- Dificuldade de Inversão: É fácil calcular um ponto na curva, mas extremamente difícil calcular a origem desses pontos.
- Ponto de Adição: A soma de dois pontos na curva também resulta em um ponto na curva.
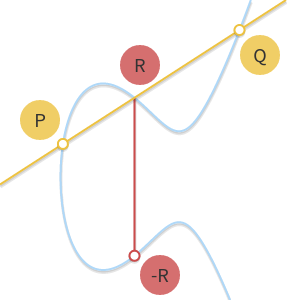
- Multiplicação Escalar: Multiplicar um ponto por um número escalar resulta em outro ponto na curva, mas reverter essa operação (encontrar o número escalar a partir dos pontos resultantes) é computacionalmente difícil.
Chave Privada de Bitcoin
Uma chave privada de Bitcoin é uma sequência de 256 bits, o que significa que há \(2^{256}\) combinações possíveis. No entanto, a segurança efetiva é de 128 bits devido às propriedades matemáticas das curvas elípticas. Isso ainda representa um número astronômico de combinações, tornando a chave privada extremamente difícil de ser quebrada por ataques de força bruta na era atual.
128 bits de segurança: Este é o nível de segurança efetivo contra ataques de força bruta, devido às propriedades matemáticas das curvas elípticas.
Para colocar isso em perspectiva, quebrar uma chave com 128 bits de segurança exigiria, em média, \(\approx 2601150623552800702891545856\) tentativas - um número que ainda está além das capacidades computacionais atuais, igualmente ao número de tentativas para tentar decifrar uma seed phrase de 24 palavras, utilizando o método birthday attack.
Ataques às Chaves Privadas em Curvas Elípticas
No campo da criptografia, ataques avançados como o algoritmo de Pollard's rho e o método Baby-step Giant-step representam ameaças teóricas à segurança da chaves privadas. Esses métodos são sofisticados e requerem uma compreensão profunda dos princípios matemáticos que fundamentam a criptografia de curvas elípticas.
Algoritmo de Pollard's Rho
O algoritmo de Pollard's rho é um método de fatoração de inteiros e de resolução do problema do logaritmo discreto. Ele é usado para encontrar colisões em funções de hash e para resolver o problema do logaritmo discreto como os utilizados na criptografia de curvas elípticas.
Como Funciona:
- Caminho Aleatório: O algoritmo utiliza um caminho aleatório para encontrar uma colisão. Imagine uma caminhada aleatória sobre os pontos da curva elíptica, onde eventualmente, por causa do paradoxo do aniversário, dois pontos diferentes levarão ao mesmo ponto na curva.
- Detecção de Ciclos: Pollard's rho detecta ciclos no caminho aleatório usando a técnica de tortoise and hare, onde dois ponteiros (um lento e um rápido) eventualmente colidirão.
- Cálculo do Logaritmo Discreto: Uma vez que uma colisão é encontrada, pode-se resolver o logaritmo discreto, quebrando assim a chave privada.
Método Baby-step Giant-step
O método Baby-step Giant-step é um algoritmo de força bruta otimizado para resolver o problema do logaritmo discreto. Ele divide o problema em dois passos, reduzindo o espaço de busca.
Como Funciona:
- Divisão do Espaço de Busca: O problema do logaritmo discreto \(P = kG\) é dividido em duas partes:
- Baby Steps: Calcula-se uma tabela de \(m\) valores de \(kG\), onde \(m\) é a raiz quadrada do tamanho do grupo.
- Giant Steps: Busca-se um valor na tabela que corresponda ao objetivo, usando passos maiores (saltos gigantes).
- Combinação de Resultados: A combinação das duas tabelas permite resolver o logaritmo discreto de forma eficiente.
Exemplo Prático
Para um grupo de ordem \(N\), o método Baby-step Giant-step requer cerca de \(2 \sqrt{N}\) operações, o que é significativamente mais rápido que a abordagem de força bruta direta. No contexto das curvas elípticas utilizadas no Bitcoin, isso ainda representa uma quantidade massiva de cálculos, mas é mais eficiente que outras abordagens.
Estudos de Caso e Exemplos Históricos
Embora esses métodos sejam teoricamente viáveis, sua aplicação prática em contextos atuais de criptografia de curvas elípticas é limitada devido ao enorme poder computacional necessário. No entanto, existem exemplos históricos onde variantes desses métodos foram explorados:
- Quebra do MD5 e SHA-1: Técnicas similares foram usadas para encontrar colisões em algoritmos de hash mais fracos, como MD5 e SHA-1. Esses ataques demonstraram a viabilidade dos métodos em algoritmos que não oferecem segurança suficiente.
- Concursos de Criptografia: Várias competições de criptografia e desafios matemáticos têm explorado o uso desses algoritmos para resolver problemas específicos, incentivando a pesquisa e o desenvolvimento de técnicas mais eficientes.
A Era Pré-Quântica e a Segurança Criptográfica
O horizonte da segurança criptográfica está mudando com o avanço da computação quântica. Computadores quânticos, quando suficientemente poderosos, poderão usar o algoritmo de Shor para quebrar a criptografia de curva elíptica em um tempo significativamente menor do que os computadores clássicos. Neste contexto, é fundamental entender o impacto potencial da computação quântica na criptografia e os esforços atuais na criptografia pós-quântica.
O Algoritmo de Shor
Desenvolvido por Peter Shor em 1994, o algoritmo de Shor é um algoritmo de fatoração de inteiros que pode resolver eficientemente o problema do logaritmo discreto (DLP). Ele é particularmente eficaz contra criptografia de chave pública, como a RSA e as curvas elípticas, que dependem da dificuldade de fatorar grandes números inteiros ou resolver logaritmos discretos.
Funcionamento do Algoritmo de Shor
- Entrada: Um número inteiro composto (N).
- Saída: Os fatores primos de (N).
- Processo:
- Usa um computador quântico para encontrar o período de uma função específica relacionada ao número (N).
- Converte o problema de fatoração em um problema de encontrar o período de uma função, que pode ser resolvido eficientemente por um computador quântico.
Impacto na Criptografia
A criptografia de curvas elípticas, como a usada pelo Bitcoin, depende da dificuldade de resolver o problema do logaritmo discreto em uma curva elíptica. O algoritmo de Shor pode resolver este problema de maneira eficiente com um computador quântico suficientemente poderoso, ameaçando a segurança das chaves privadas utilizadas atualmente.
Janela de Tempo
Atualmente, não existem computadores quânticos capazes de quebrar a criptografia do Bitcoin. Estimativas variam, mas muitos especialistas acreditam que levará de 10 a 20 anos para desenvolver computadores quânticos que representem uma ameaça real.
Criptografia Pós-Quântica
Diante dessa ameaça futura, a comunidade criptográfica já está desenvolvendo algoritmos resistentes a ataques quânticos. Estes novos algoritmos são projetados para serem seguros contra as capacidades computacionais dos futuros computadores quânticos.
Algoritmos Pós-Quânticos
Alguns dos algoritmos pós-quânticos que estão sendo pesquisados incluem:
- Lattice-based Cryptography: Baseado na dificuldade de resolver problemas em lattices.
- Multivariate Polynomial Cryptography: Utiliza a dificuldade de resolver sistemas de equações polinomiais multivariadas.
- Hash-based Cryptography: Baseado na segurança das funções hash.
Quando necessário, esses algoritmos poderão ser implementados no Bitcoin e em outras criptomoedas para garantir sua segurança. A transição para criptografia pós-quântica exigirá atualizações nos protocolos e software das criptomoedas, mas é uma área ativa de pesquisa e desenvolvimento.
Segurança Pré-Quântica
Por enquanto, estamos seguros na era pré-quântica. A tecnologia atual não permite que computadores quânticos realizem ataques eficazes contra a criptografia de curvas elípticas. Até que os computadores quânticos avancem a ponto de se tornarem uma ameaça prática, medidas de segurança robustas, como o uso de seed phrases de 24 palavras, continuam a oferecer uma ampla margem de segurança.
A Importância de uma Passphrase Forte
Para garantir a segurança de suas criptomoedas, uma passphrase forte é crucial. A força de uma passphrase é medida pela quantidade de bits de entropia, que é uma representação da imprevisibilidade ou aleatoriedade de uma senha. Quanto maior a entropia, mais difícil é adivinhar a senha. Cada bit adicional de entropia dobra o número de possíveis combinações, tornando a tarefa de um invasor exponencialmente mais difícil.
Por exemplo, uma senha com 42 bits de entropia requer \(2^{42}\) (ou aproximadamente 4,39 trilhões) de tentativas para ser quebrada por força bruta. Adicionar um bit extra de entropia aumenta esse número para \(2^{43}\) (ou cerca de 8,79 trilhões), dobrando a segurança. Assim, uma senha de 43 bits de entropia requer o dobro de tentativas para ser descoberta em comparação com uma senha de 42 bits.
Um ponto importante a considerar é a distinção entre entropia e força da senha. A entropia é uma medida válida da aleatoriedade de uma senha, mas não é uma medida direta de sua força. Por exemplo, a senha zzzzzzzzzz,zzzzzzzzzzzzz*zzzzzzzzzzzzzzz possui uma entropia baixa, pois contém apenas três caracteres distintos, mas ainda é muito improvável de ser quebrada. Por quê? Porque um invasor não sabe que sua senha contém apenas três caracteres distintos e, portanto, realizaria um ataque de força bruta baseado na suposição de uma entropia maior. O tamanho da senha ajuda a compensar a entropia fraca.
Para senhas curtas, a entropia é crítica na determinação da força da senha. No entanto, a verdadeira medida da força de uma senha é o número de permutações necessárias para realizar um ataque de força bruta. Enquanto a gama de conjuntos de caracteres determina as permutações, o comprimento da senha também desempenha um papel importante.
Além da seed phrase, a implementação de uma passphrase adicional, também conhecida como "seed extension" ou "25ª palavra", pode aumentar significativamente a segurança. Uma passphrase deve ter alta entropia para ser eficaz. Aqui estão algumas diretrizes para criar uma passphrase forte:
- Comprimento: A passphrase deve ter idealmente 20 ou mais caracteres.
- Complexidade: Inclua uma mistura de letras maiúsculas e minúsculas, números e símbolos.
- Aleatoriedade: Evite usar palavras comuns ou sequências previsíveis. Use caracteres aleatórios.
- Memorabilidade: Não tente memorizá-la, pois existe o risco de acidentes e/ou doenças e você ter problemas com a sua memória. Armazene a sua passphrase de maneira segura.
wH<*j+%FJ=7$o?[PowG}gyc[VrEEU?(exemplo para demonstração, jamais utilize esta passphrase).
Utilizar uma seed phrase de 24 palavras em combinação com uma passphrase forte adiciona uma camada de segurança que requer tanto "algo que você tem" (a seed phrase) quanto "algo que você sabe" (a passphrase). Essa abordagem de segurança de dois fatores torna a tarefa de um invasor significativamente mais difícil.
Portanto, ao proteger suas criptomoedas, escolha sempre uma seed phrase de 24 palavras e combine-a com uma passphrase forte para garantir a máxima segurança dos seus ativos digitais.
Boas Práticas para Gerenciamento de Passphrases
Armazenamento Seguro: Armazene sua senha offline ou utilize um gerenciador de senhas offline e localmente, para armazenar suas passphrases de maneira segura.
Backup: Faça backup de suas passphrases em locais seguros, como um cofre físico ou uma mídia offline.
Evite Reutilização: Não reutilize a mesma passphrase para múltiplas contas ou serviços.
Atualizações Regulares: Embora não seja possível atualizar a passphrase da sua wallet Bitcoin, atualize a passphrases de acesso a outros serviços periodicamente e sempre que suspeitar que possam ter sido comprometidas.
Ferramentas para Gerar e Gerenciar Passphrases
Geradores de Passphrases:
Existem várias ferramentas online e offline que podem ajudar a gerar passphrases fortes e aleatórias:
- Diceware: Um método que usa dados físicos para gerar palavras aleatórias a partir de uma lista predefinida.
- Assista ao vídeo no canal Bitcoinheiros em que o BitDov dá um ótimo exemplo de como criá-las.
Armazenamento Offline
Armazenamento offline é a forma mais robusta e segura de proteger seu Bitcoin e outros criptoativos. Ao escolher esta modalidade, é crucial realizar backups em múltiplos locais e utilizar mídias duráveis, como metal. Existem diversos modelos de metal wallet disponíveis no mercado brasileiro para atender a essa necessidade.
Gerenciadores de Senhas:
Os gerenciadores de senhas são ferramentas muito úteis para armazenar e organizar suas passphrases de maneira segura, desde que offline e em um computador dedicado à essa tarefa:
- KeePassXC: Um gerenciador de senhas gratuito e de código aberto que oferece armazenamento seguro de senhas. Ele pode operar localmente, sem conexão com a Internet. Também suporta várias plataformas e permite a sincronização de senhas através de serviços de armazenamento em nuvem (não recomendado).
Segurança Prática
Na prática, isso significa que a chave privada está altamente protegida contra ataques diretos. Os vetores de ataque mais prováveis não são matemáticos ou criptográficos, mas sim:
- Engenharia social: Manipulação psicológica para obter informações sensíveis.
- Phishing: Tentativas de enganar usuários para revelar suas chaves privadas.
- Malware: Software malicioso projetado para roubar informações do dispositivo do usuário.
- Armazenamento inseguro: Guardar a seed phrase ou chave privada de forma não criptografada em locais vulneráveis.
Conclusão: 12 vs 24 Palavras: Qual Escolher?
A escolha entre uma seed phrase de 12 ou 24 palavras é crucial para a segurança de suas criptomoedas. A recomendação clara é optar por 24 palavras, apesar do pequeno inconveniente de registrar mais palavras. A compensação é uma segurança exponencialmente maior.
Quando desconsideramos o ataque de aniversário, podemos ser induzidos a uma falsa sensação de segurança, imaginando que o número de bits necessários para um ataque de força bruta é equivalente à quantidade de bits de segurança da chave privada: \(2^{128}\). À primeira vista, pode parecer que ambas oferecem a mesma proteção.
No entanto, a realidade é que uma seed phrase de 24 palavras oferece uma segurança comparável à da chave privada em um cenário de ataque de aniversário: \(2^{128}\), enquanto uma seed phrase de 12 palavras tem sua segurança drasticamente reduzida para \(2^{64}\).
Embora explorar tal ataque exija um poder computacional extremamente elevado, é prudente adotar medidas preventivas diante do rápido avanço da tecnologia. Assim como seguimos a boa prática de não reutilizar wallets, mesmo considerando que tais ataques sejam impraticáveis nos dias de hoje, proteger seus recursos contra possíveis ameaças futuras é essencial.
É crucial lembrar que ataques diretamente à chave privada ainda dependem da exposição da chave pública e só se tornarão viáveis com a chegada dos computadores quânticos, algo esperado para um futuro de longo prazo. No entanto, os ataques de aniversário dependem apenas de um grande poder computacional tradicional, pré-quantum, e do sucesso do Bitcoin com muitos usuários e wallets para serem executados com sucesso.
Portanto, adotar uma seed phrase de 24 palavras, acompanhada de uma passphrase forte, é uma medida essencial para garantir a segurança de suas criptomoedas em um cenário de rápida evolução tecnológica.


